library(MASS)
library(gutenbergr)
library(tidytext)
library(topicmodels)
library(tm)
library(ggplot2)
library(dplyr)
library(lda)

Clustering

Mixture models suggest a distribution might represent several types of individuals. In some of our courses we see a grade distribution with multiple modes or if we go with a classic \(Y_i\) is the velocity of the \(i^{th}\) galaxy.

# this is the only time we will use the MASS library
hist(MASS::galaxies,35)

We often interpret this as being a heterogeneous group where there are subgroups, perhaps modelling them as: \[P(Y_i\mid\theta,\sigma, p) = \sum_{k=1}^{K} p_k N(Y_i\mid\theta_k,\sigma^2_k).\] Although there is a single population, we think of individuals as belonging to different subgroups.

Most clustering relies on this concept and tries to find the subgroups based on groups of individuals who are more similar to each other than they are to the other groups.

It’s natural to think of an individual as being a member of a single group so that the problem simplifies if we can condition on group membership \(Z\). \[P(Z_i=k\mid p_k)=p_k\] \[P(Y_i\mid Z_i=k,\theta,\sigma, p) = N(Y_i\mid\theta_k,\sigma^2_k)\] \[P(Y_i, Z_i=k\mid \theta,\sigma, p) = p_k N(Y_i\mid\theta_k,\sigma^2_k)\] \[P( Z_i=k\mid Y_i,\theta,\sigma, p) = \frac{ p_k N(Y_i\mid\theta_k,\sigma^2_k)}{ \sum_{j=1}^{K} p_j N(Y_i\mid\theta_j,\sigma^2_j)}\]

Soft (or fuzzy) clustering instead considers each individual to be divided between some or all of the groups. Statistically, we model individual as having a Dirichlet allocation model dividing it between groups.

LDA

In Latent Dirichlet Allocation (LDA), each document has a latent allocation of topics. This document might be 39% computing and 60% statistics, but only 1% recipes. Each topic has a categorical distribution providing probabilities for all the words. The statistics topic would likely have a very low probablitity of the word borscht, but a high probability allocated to words like distribution and Dirichlet.

The original LDA method comes from this exceedingly high impact paper: D.Blei, A. NG, M. Jordan (2003) “Latent Dirichlet Allocation”, JMLR. There are many variants and computational improvements, but we’ll focus here anyways.

LDA was constructed based on a generative process for each document in a corpus. Each document is considered a bag of words, so word order is ignored.

Generative model

Sample a word allocation distribution for each topic \(\phi_k\sim Dir(\beta)\), for the \(k=1,...,K\) topics.
For document \(d\) sample a topic allocation \(\theta_d\sim Dir(\alpha)\). These are the topic proportions for this document.
For each word \(w_n,\ n\in 1,...,N_d\) in document \(d\):
1. Sample its topic \(z_{dn} \sim Multinomial(\theta_d)\). The \(n^{th}\) word position in document \(d\) has a single latent topic \(z_{dn}\).
2. Sample a word \(w_n\) from \(p(w_n \mid \phi_{z_{dn}})\), a categorical probability disribution with word probability \(\phi_{z_{dn}}\) that is specific to the topic \(z_n\).

As a graphical model for what the original Blei paper called smoothed LDA (although they used slightly different notation, the above is pretty standard notation) 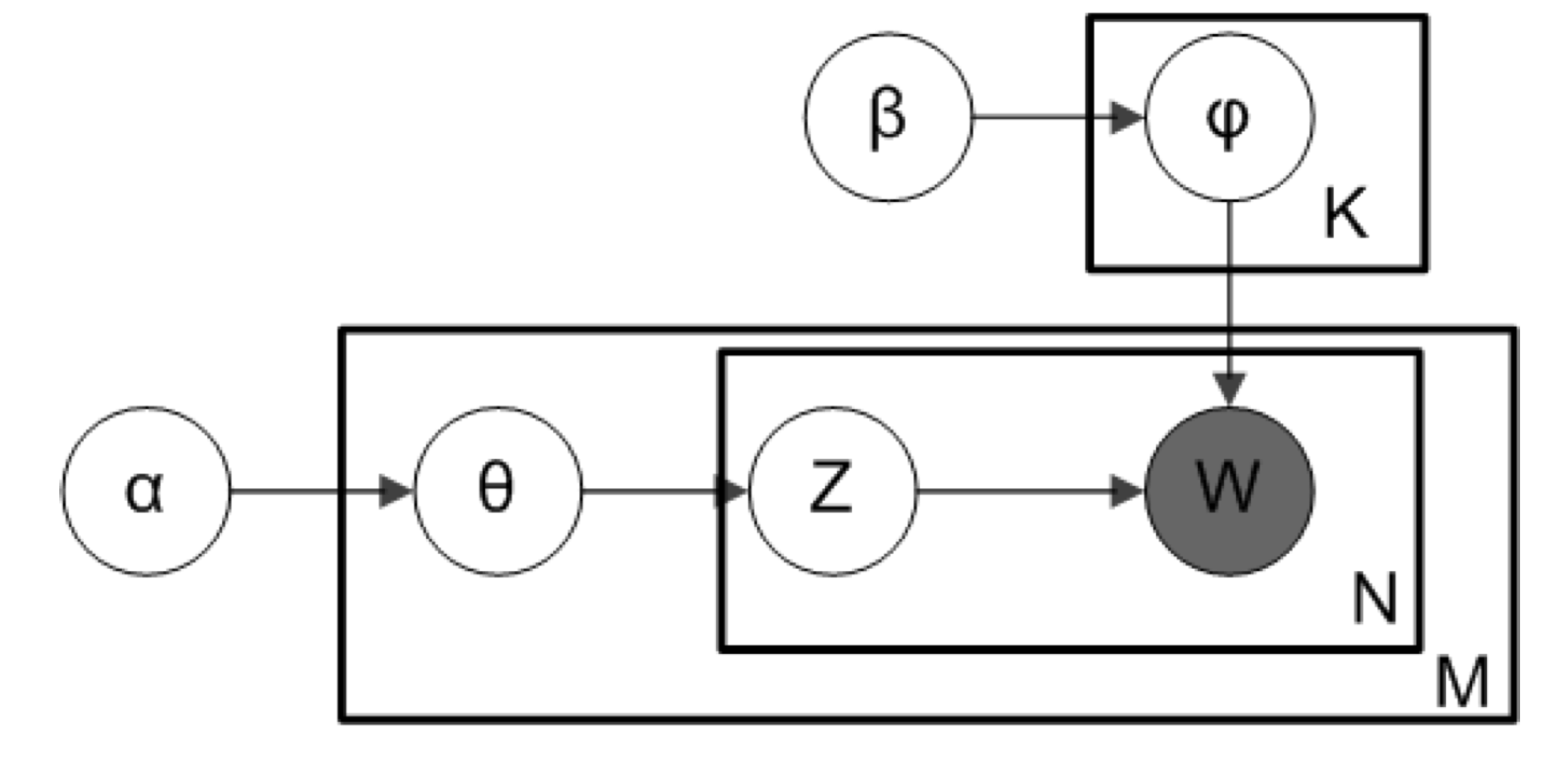LDAmodel

Many variations of LDA exist.

Of interest is interpreting the topic allocations \(\theta\). We might be interested in expanding the model to do inference, but… we’ll come back to that.

Clustering books

Let’s start with an obvious example taking some books from Gutenberg.


Wells = gutenbergr::gutenberg_works(author =="Wells, H. G. (Herbert George)")
Wells

Montgomery = gutenbergr::gutenberg_works(author =="Montgomery, L. M. (Lucy Maud)")
Montgomery

Dickens = gutenbergr::gutenberg_works(author =="Dickens, Charles")
Dickens

Consider a selection of 3 books from each author

#Wellsbooks = gutenberg_download(c(36,3797,5230,1138,775), meta_fields = c("title","author"))
Wellsbooks = gutenberg_download(c(36,1138,5230), meta_fields = c("title","author"))
unique(Wellsbooks$title)
#Montgomerybooks = gutenberg_download(c(45,51,544,5341,5343), meta_fields = c("title","author"))
Montgomerybooks = gutenberg_download(c(45,51,544), meta_fields = c("title","author"))
unique(Montgomerybooks$title)
#Dickensbooks = gutenberg_download(c(776,730,786,1400,1392 ), meta_fields = c("title","author"))
Dickensbooks = gutenberg_download(c(46,98,730 ), meta_fields = c("title","author"))
unique(Dickensbooks$title)

Let’s split books into chunks and treat chunks as documents. It doesn’t matter how long a document is, but working with book chapters will have a short compute time compared to bringing in more than 9 books to cluster.

AllBooks = rbind(Wellsbooks,Montgomerybooks,Dickensbooks)

tidy_books = AllBooks %>%
       group_by(title) %>%      #  group by 
         mutate(linenumber = row_number(),
              chapter = cumsum(str_detect(text, regex("(^chapter\\s+)|(^stave\\s+)|(^[\\divxlc]+(\\.|$))",ignore_case = TRUE)))) %>%
             ungroup() %>%
                unnest_tokens(word, text)  %>%
                filter(!(gutenberg_id==46 & linenumber<33))   # The table of contents oteherwise folds into very short chapters

Sometimes we get rid of stopwords before converting into document term matrix. This depends a lot on the context.

Stop word libraries

# small library that is hard to not like:
tm::stopwords()

# 3 different stop word lexicons that depend on your context:
tidytext::stop_words
table(tidytext::stop_words$lexicon)

We could further build up character names in the list of stopwords, but in real life we may be more interested in performing this clustering on insurance reports, court documents, and proper names shouldn’t matter as they amount to noise in the documents.

It is impossible to separate apart data cleaning from analysis when dealing with text data. With any data type, automated data cleaning will have unintended consequenses, but with text we should think carefully about (and assess) their impact.

# build my own stop words to include single letter words
stops = data.frame(word = c(tm::stopwords(), letters) )


wordcount = tidy_books %>%
 anti_join(stops) %>%
 filter(chapter !=0) %>%            # get rid of preamble 
  group_by(title,chapter,author) %>%       # count within a chapter in a document                        
  count(word,sort=TRUE)%>% 
  ungroup() %>% 
  unite("document", title:chapter)   # make a new column with document  = title + chapter

  DTM = wordcount %>% cast_dtm(term=word,document=document,value=n)

The document term matrix has one row per document and one colum per word. Matrix entries are the counts of word occurence within a document. The matrix is almost always very sparse.

Model Fitting

It’s natural to think of fitting a Latent Dirihlet Allocation model using Bayesian sampling techniques. Indeed we generally use Gibbs sampling or Variational methods to do this.

The joint distribution over the specific words within the documents \(W=[w_1,...]\), topics for those words \(Z=[z_1,...]\), topic allocations for the \(D\) documents \(\theta=[\theta_1,...,\theta_D]\), and word allocation distribution within each of the \(K\) topics \(\phi=[\phi_1,...\phi_K]\) is

\[P(W,Z,\theta,\phi\mid \alpha, \beta) = \prod_{i=1}^KP(\phi_k\mid \beta) \prod_{j=1}^MP(\theta_j\mid \alpha) \prod_{t=1}^{N_j}P(z_{j,t}\mid \theta_j)P(w_{jt}\mid\phi_{z_{jt}}).\]

# takes about 11 seconds
k = 3

LDA3 = topicmodels::LDA(DTM, k,method = "VEM")  #original code from the Blei et al 2003 paper
LDA3 = topicmodels::LDA(DTM, k,method = "Gibbs") #collapsed Gibbs came after the Blei paper

About those samples

At this point you are probably wondering why I didn’t specify the number of Gibbs samples and the burn in,… Well, often in literature and in practice people report using 20,000ish Gibbs samples. Sorry that’s a typo, it should be 20ish Collapsed Gibbs samples. In general Collapsed Gibbs sampling is used as a stochastic optimizer and get close to a local mode. The only part returned is the final iteration of the sampler. The collapsed part means that we marginalize over some parameters and then estimate those marginalized parameters afterwards.

We typically marginalize over topic allocations and word within topic allocations \[P(z, w\mid \alpha, \beta) = \int \int P\left(z,\phi_{z},\theta, w\mid \alpha, \beta\right)d\theta d\phi,\]

All of the Collapsed Gibbs Sampling then reduces to a simpler problem that could be thought of as having a likelihood term \(P(w_{dn}\mid z_{dn})\) and a hierarchical model for the word specific topic allocations \(P(z_{dn}\mid \alpha, \beta)\).

Collapsed Gibbs scales well, can be distributed nicely, and converges quickly. However, in practice, convergence is not towards a target distribution but rather to something close to an optimum.

For Document d, topic k, word index n, and vocabulary of size V after the sampler has burned-in, estimate:

\[\hat{\theta}_{dk}\approx \frac{\sum_n^{N_d}I\!I(z_{dn}=k) +\alpha_k}{\sum_{i=1}^K \sum_n^{N_d}I\!I(z_{dn}=k) +\alpha_n}\]

\[\hat{\phi}_{kv}\approx \frac{\sum_{d=1}^M\sum_{n}^{N_d} I\!I(w_{dn}=v \&z_{in}=k)+\beta_v}{\sum_{r=1}^V \sum_{d=1}^M\sum_{n}^{N_d} I\!I(w_{dn}=r \&z_{dn}=k) + \beta_r}\]

Samplers have to deal with an enormous label switching problem rendering inference on \(\theta\) or \(\phi\) complex and essentially useless unless one can condition on some sort of topic structure. As a result you won’t be able to get the (Collapsed) Gibbs samples from any of the software, they just return \(\hat{\theta}\) and \(\hat{\phi}\).

Variational methods directly target \(\theta\) and \(\phi\) and are used but Collapsed Gibbs tends to be fastest at larger scales.

Some insight from our book clustering

Their \(\beta\) = our probability of a word given a topic


tidy_lda = tidy(LDA3)
top_terms = tidy_lda %>%
  group_by(topic) %>%
  top_n(20, beta) %>%
  ungroup() %>%
  arrange(topic, -beta)
top_terms

Or in plots:



top_terms %>%
  mutate(term = reorder_within(term, beta, topic)) %>%
  group_by(topic, term) %>%    
  arrange(desc(beta)) %>%  
  ungroup() %>%
 
 
 ggplot(aes(term, beta, fill = as.factor(topic))) +
  geom_col(show.legend = FALSE) +
  coord_flip() +
  scale_x_reordered() +
  labs(title = "Top  terms in each  topic",
       x = NULL, y = expression(beta)) +
  facet_wrap(~ topic, ncol = 4, scales = "free")

Their \(\gamma\) = our probability of topic within document

lda_gamma =  tidy(LDA3, matrix = "gamma")

lda_gamma$title =  stringr::str_replace_all(lda_gamma$document, pattern="\\_\\d+", replacement = "")
lda_gamma

 lda_gamma %>% left_join(unique(AllBooks[,c("title","author")])) %>%
  mutate(title = reorder(title, gamma * topic)) %>%
  ggplot(aes(factor(topic), gamma,fill = as.factor(author))) +
  geom_boxplot() +
  labs(title = "Topic allocations for chapters within books",
       x = "topic", y = "topic allocation") +
  facet_wrap(~ title)

Further tricks

If all the documents right now were from newspapers terms like George_Floyd show up in every article. They could be considered stopwords. You could also use tf_idf to find and suggest new stopwords, but it doesn’t matter with LDA. Exceedingly common terms either become pushed into a very common topic that appears heavily weighted across all documents or these terms show up as being exceedingly likely within all topics. In the latter case, the more interesting and distinguishing words then appear further down the prevalence within a topic.
Selecting the number of topics. Typically one would use perplexity. We split the data into training and testing data. The LDA model is built on the training data, then perplexity is calculated over the testing data set for a variety of \(K\) values. Perplexity is the geometric mean per word likelihood, examining the probability of the words given topic allocation structure and words within topics.
\[Perplexity(Doc_{test},K) = exp\left\{-\frac{\sum_{doc}log(p(w\mid\theta,\phi))}{\sum_{doc}\{\#\mbox{words in doc}\}}\right\}\] Low scores of perplexity occur when testing documents are easily allocated to few topics with highly probable words. Perplexity measures how well new documents fit into the topic partitions and hense the ability to compress the data. In soft clustering like LDA, we often want interpretable clusters which are easier with more clusters than perplexity would suggest.
Short documents (like Twitter) are too sparse for LDA to be directly useful. Finding ways of clustering tweets is an active area of research. More words are better, especially with a large vocabulary.

Inference, tl;dr we have some but there remain open problems.

Inference is tricky with LDA. One could try to include covariates into the topic allocations, but it isn’t clear how to estimate them appropriately. Small changes in topic allocations require changes in word allocation and will blur any inference when taking a fully parameterized approach. This is an open area of research.
LDA and topic allocations are selected to be parsimonius for the documents but, like principal components, may not be optimal for use in further analysis. Supervised LDA is a model that finds optimal topics that best predict a new variable \(Y\). This is akin to rotating principal components because only a small portion of variation in X is responsible for prediction of Y. The slda.em function from library lda simultaneously fits topics and a linear model or GLM to estimate Y.

The LDA function in the library topicmodels is the easiest to get started with. However, you have much more control with library lda and its lda.collapsed.gibbs.sampler function, but the data structure is quite different. Rather than working directly with the document term matrix, it takes as input the sequence of words but written as indexes of the vocabulary vector (starting from index 0).

To sketch out the set up for our books we would need to do the following:

vocab = unique(tidy_books$word)

Docs = tidy_books %>% group_by(title, author, chapter) %>%
          mutate(document = paste(word, collapse = " ")) %>% # un-tokenize back into chapters of text (our documents)
         dplyr::select(-word) %>%   # get rid of the now redundant "word" column
         filter(row_number()==1)    # since all rows within a chapter are the same, keep only the first one

doclist = strsplit(tolower(Docs$document),"\\s")

# now build a time series of vocabulary indices that can be used to reconstruct the original text:

get_terms = function(x, vocab) {
  index   = match(x, vocab)
  index   = index[!is.na(index)]
  rbind(as.integer(index - 1), as.integer(rep(1, length(index))))
}
documents = lapply(doclist, get_terms, vocab)
# Note that the vocabulary index needs to start with index 0 since it is passed to C 
# Indexing in R begins with index 1
# Check that you can map the time series of vocabulary back to the original phrase

vocab[documents[[1]][1,]+1]

From here you can use documents and vocab as inputs to the library(lda) functions like lda.collapsed.gibbs.sampler and slda.em.

Help! let’s do another example

Saving some time by loading Beatles lyrics (from genius)

load("content/post/LookAt_yeartrackalbum.RData")

The Beatles released records with different titles in the US and UK, so in obtaining their discography I ended up with some duplicates. Focusing on their UK releases we get rid of this problem.


UKalbums = c("Please Please Me",
                "With the Beatles",
                "A Hard Day's Night",
                "Beatles for Sale",
                "Help!",
                "Rubber Soul",
                "Revolver",
                "Sgt. Pepper's Lonely Hearts Club Band",
                "Magical Mystery Tour",
                "Yellow Submarine",
                "Abbey Road",
                "Let It Be")

# we could but won't remove stop words
# songs typically have a small vocabulary so agressive stopword removal causes big problems by making th eDTM very sparse.
#stops = data.frame(word=tm::stopwords())                
#stops = tidytext::stop_words               
wordcount = yeartrackalbum  %>%  filter(album %in% UKalbums) %>% #just UK releases
  unnest_tokens(output = word, input = songlyric) %>%
  #anti_join(tidytext::stop_words) %>% 
  #anti_join(stops) %>% 
  group_by(track_title,album,Year) %>% 
  count(word,sort=TRUE)%>% 
  ungroup()
DTM = wordcount %>% cast_dtm(term=word,document=track_title,value=n)  #all recycled code from earlier

# runs for <10 seconds
k=9
BeatlesLDA = LDA(DTM, k,method="Gibbs") 
topics = tidy(BeatlesLDA, matrix = "beta")




TopWords = topics %>%
  group_by(topic) %>%               # take an action within topic values
   top_n(20, beta) %>%               # find the largest  values based on the 'beta' column
  ungroup() %>%                        # stop acting within a topic
  arrange(topic, -beta)                 # sort them 

TopWords %>%
  mutate(term = reorder_within(term, beta, topic)) %>%  # Used for faceting (glue topic to term) basically make sure that topic 1 is my topic #1
  ggplot(aes(term, beta, fill = factor(topic))) +
  geom_col(show.legend = FALSE) +
  facet_wrap(~ topic, scales = "free") +
  coord_flip() +
  scale_x_reordered()

In many cases this picks out very specific songs because of the sparcity of terms. We could remove sparse words that only appear in a few topics. Ideally words like Octopus, Eggman, and MeterMaid wouldn’t be topic forming:

# remove vocabulary terms (columns) which are more than 96.7 percent zero 
DTM95 = removeSparseTerms(DTM,.967)
# selecting the threshold is a balancing act.  We only have 152 songs so a word must be in at least 5 songs to be kept.

We could have used tf_idf here, so it’s important to remember that it is impossible to remove the impact of data cleaning on the analysis.
There is at least one song with only one or two unique words that probably shouldn’t be in the mix. Sometimes with music we end up lyrical placeholders for instrumental songs.
Those songs since they are akin to outliers in simple linear regression. We will remove sparse documents, i.e. those with less than 5 words or less than 5 unique words since the latter will overemphasize some words. We could just add way more topics and then a few topics become garbage collectors capturing single documents but we do want to explore the general themes with few topics and hense short compute time.

DTM95matrix = as.matrix(DTM95)

Removethese = which(apply(DTM95matrix,1,function(x){sum(x>0)<5 | sum(x)<5}))
DTM95 = wordcount %>%  filter (!(wordcount$track_title %in% names(Removethese)))%>%
     cast_dtm(term=word,document=track_title,value=n) %>% 
     removeSparseTerms(.95)
     DTM
     DTM95
     
 # runs for <10 seconds
k=9
BeatlesLDA = LDA(DTM95, k,method="Gibbs") 
topics = tidy(BeatlesLDA, matrix = "beta")

# recycled code:

TopWords = topics %>%
  group_by(topic) %>%               # take an action within topic values
   top_n(20, beta) %>%               # find the largest  values based on the 'beta' column
  ungroup() %>%                        # stop acting within a topic
  arrange(topic, -beta)                 # sort them 

TopWords %>%
  mutate(term = reorder_within(term, beta, topic)) %>%  # Used for faceting (glue topic to term) basically make sure that topic 1 is my topic #1
  ggplot(aes(term, beta, fill = factor(topic))) +
  geom_col(show.legend = FALSE) +
  facet_wrap(~ topic, scales = "free") +
  coord_flip() +
  scale_x_reordered()

References and more to read

Using LDA on scientific papers:

Thomas L. Griffiths, Mark Steyvers, (2004) “Finding scientific topics” PNAS, 101 5228-5235 https://www.pnas.org/content/101/suppl_1/5228

Accelerating Collapsed Gibbs Sampling for LDA:

Porteous et al (2008) “Fast Collapsed Gibbs Sampling For Latent Dirichlet Allocation”, KDD https://www.ics.uci.edu/~asuncion/pubs/KDD_08.pdf

Distributed computing for LDA Qiu et al (2014) “Collapsed Gibbs Sampling for Latent Dirichlet Allocation on Spark” JMLR: Workshop and Conference Proceedings 36:17–28, http://proceedings.mlr.press/v36/qiu14.pdf